News Subscription
Here you can choose from 2 subscription methods: Shopify (default) and MailChimp. If you choose a Shopify (default) method, your subscribers will be added to your “accepts marketing” customer list. For the MailChimp method you need to have a MailChimp URL in order to have access to your subscribers’ data. Where to get MailChimp form action URL you can check here.
Subscription Popup
Enable subscription popup
If you want a subscription popup to appear, simply enable this option.
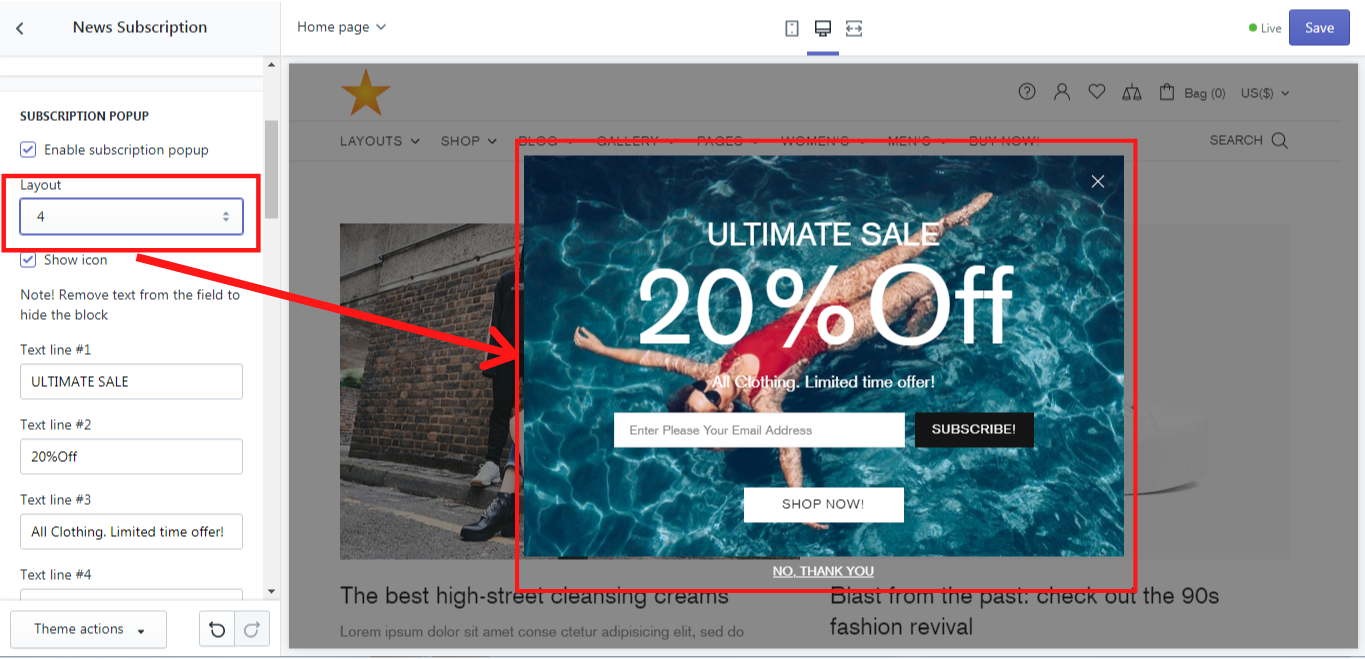
Layout
There are 5 possible layouts for the popup, which appears on the home page only. Let´s take a look at each of them:
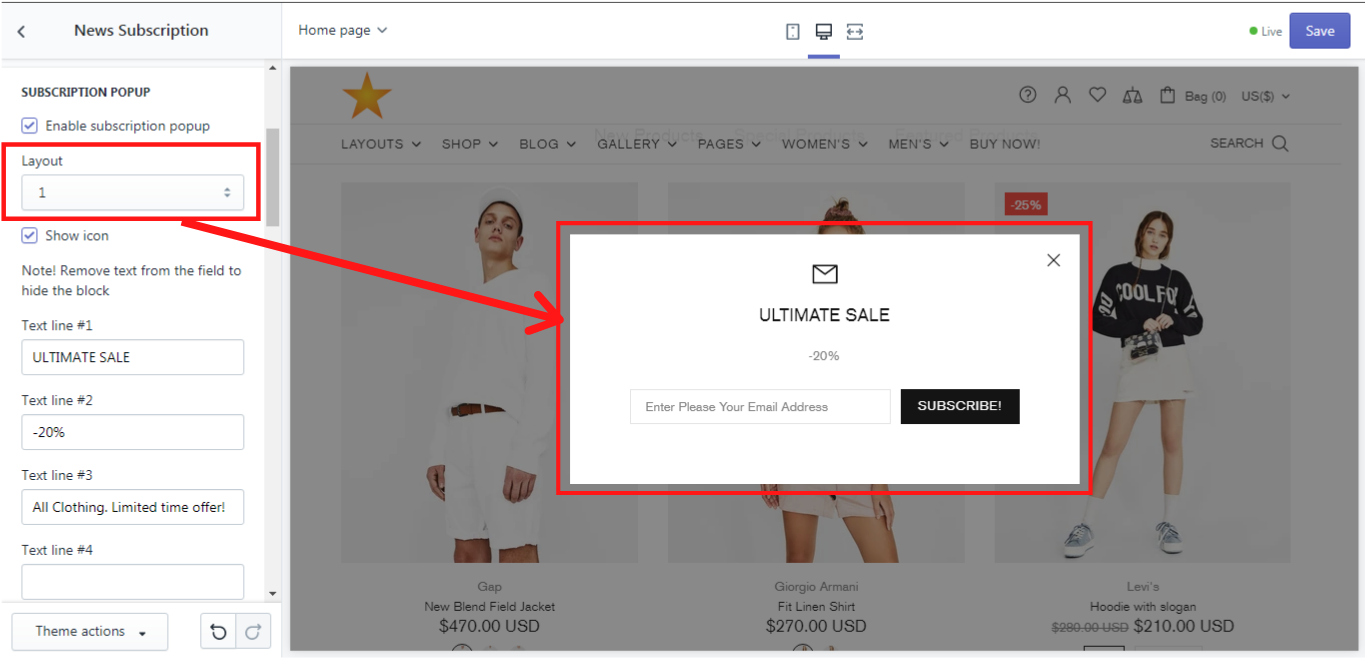
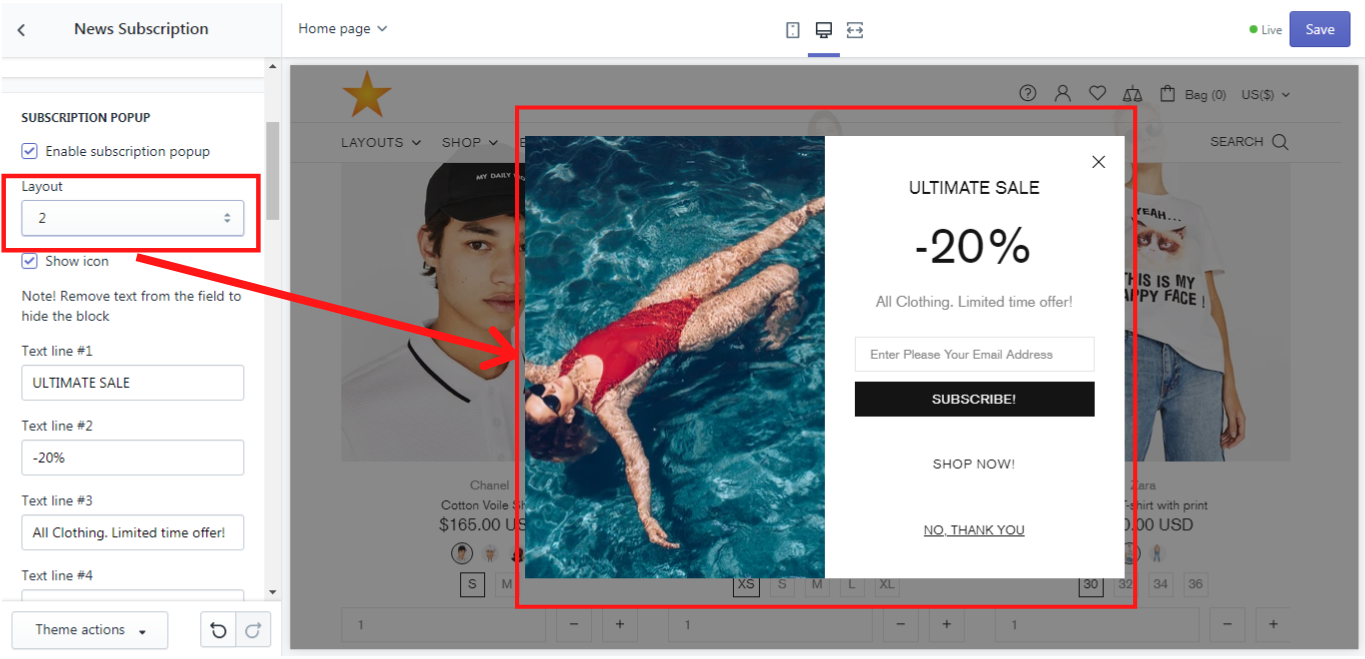
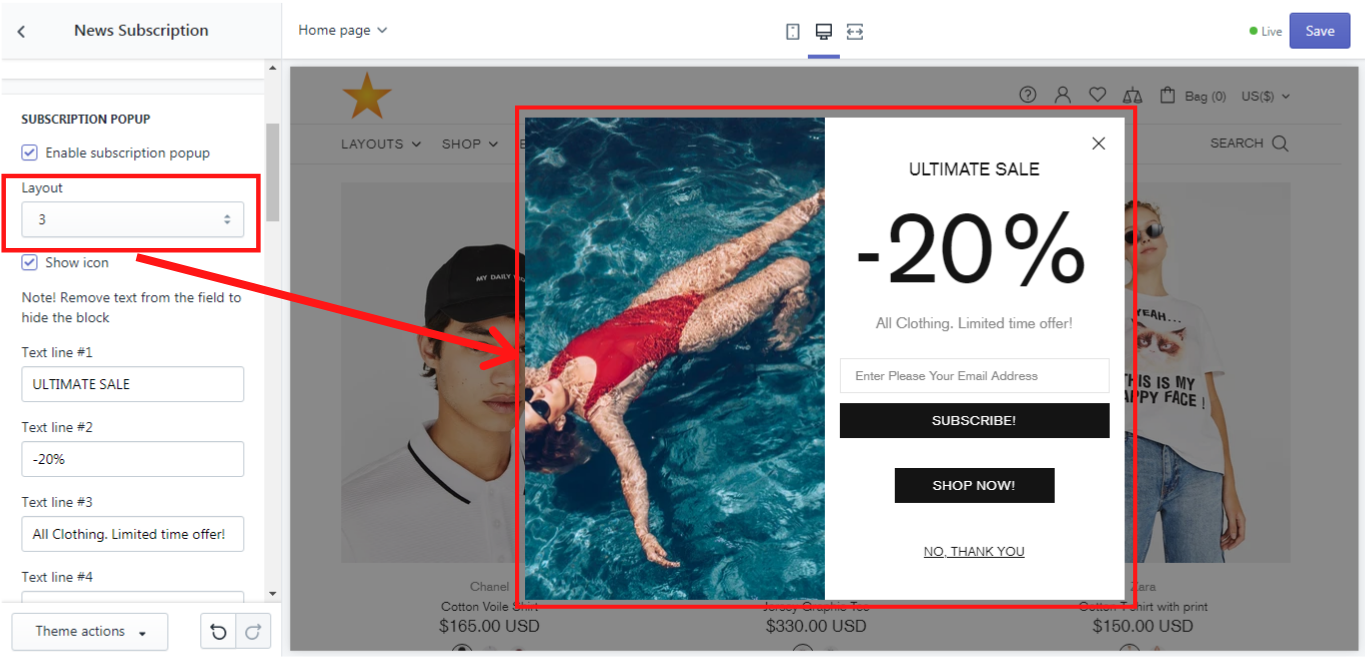
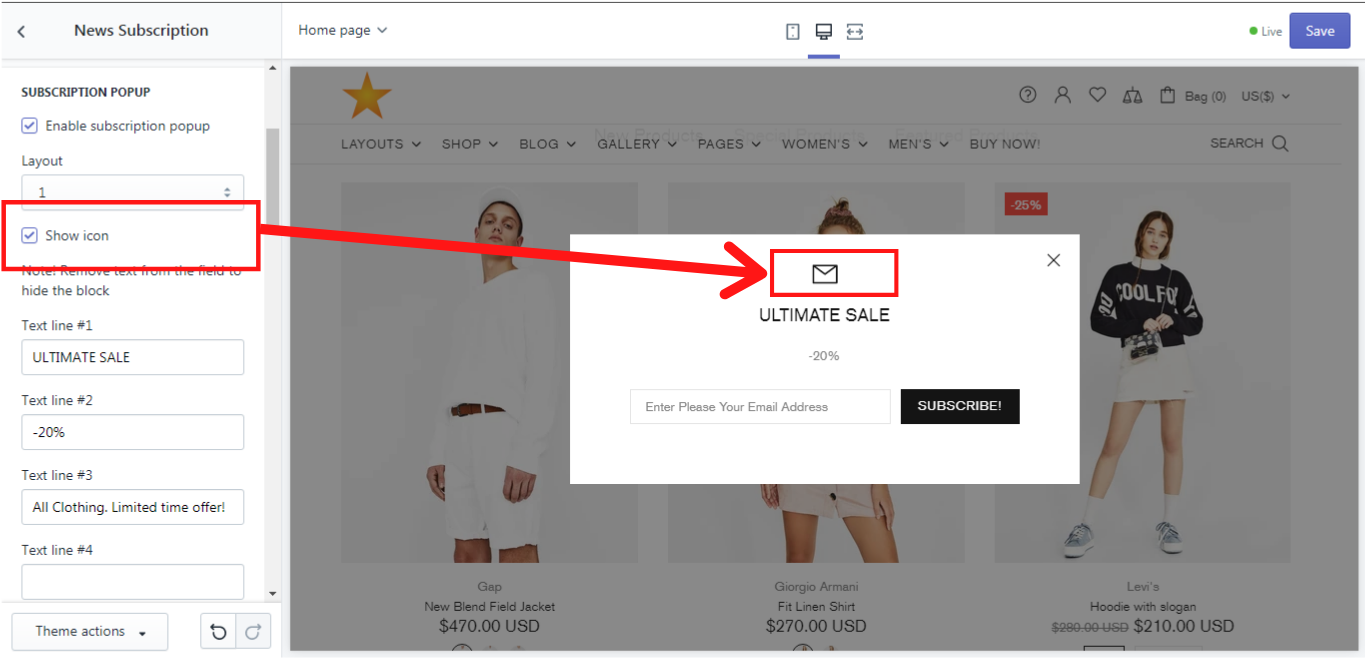
Show icon
You can decide, whether a subscription icon should be shown in the popup. This icon is visible in the Layout #1 only:
In each layout you have an option to add up to 4 text lines. Once you leave them blank, no text will be shown in the popup.
Show form
This option enables you to decide whether a subscription form should be shown in the popup.
Here you can choose any content to be displayed, e.g.: an input placeholder, a submit text button, e.g.: “SUBSCRIBE!”, a link button text, e.g.: “SHOP NOW”, the text fields for “Don´t show again” or “Close popup”.
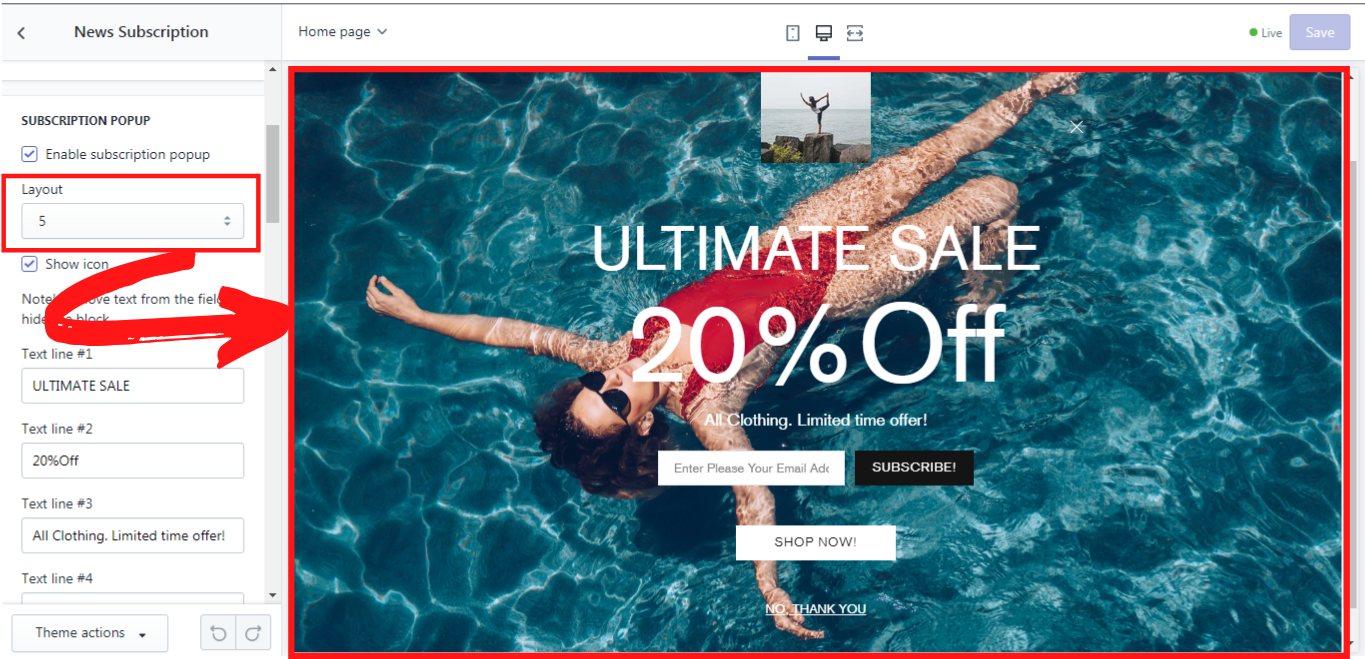
A background image can also be chosen for the subscription popup. Its width can be varied from 100 to 1200 px. An image format can be either transparent or not. Once you enable a PJPG format, the transparent images will not be shown. You can also have a second image in the popup, which is called an “Insert image”. However, this option is available for the Layout # 5 only. The width of the “Insert image” can be varied from 50 to 500 px.
Link
Here you can add a link to any store page, e.g.: Collection page, Policies, etc. Simply click on the field and a dropdown list with the available options will appear.
Show once?
Here you can decide how often the popup will be shown on the store page. There are 2 options: Once, or Unless user select “Don´t show”. Simply select one out of them.
Delay (sec)
This time scale enables you to decide in how many seconds after refreshing the page the popup should appear. The time span is from 1 to 60 seconds.
Cookies life
Here you can decide how long the system should work with the client´s cookies or how often they should be refreshed in the system. You can choose 1 day, 3 days, 1 week, 1 month, or 1 year.
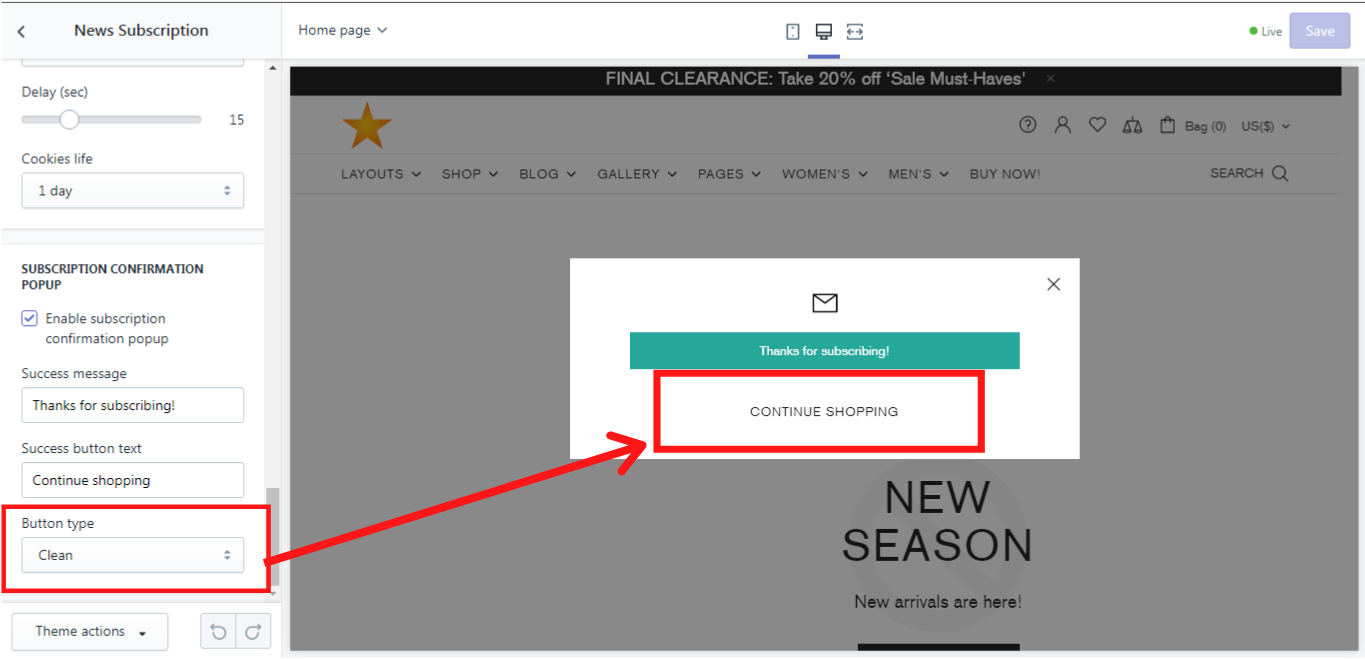
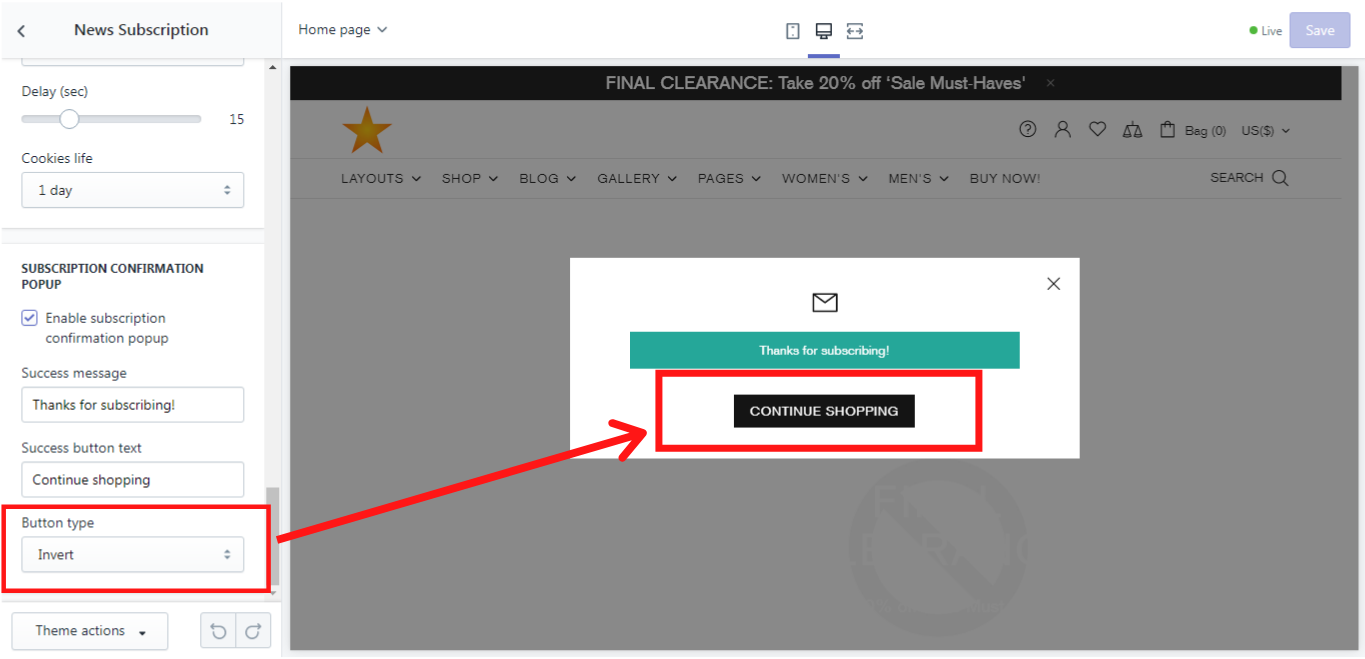
Subscription confirmation popup
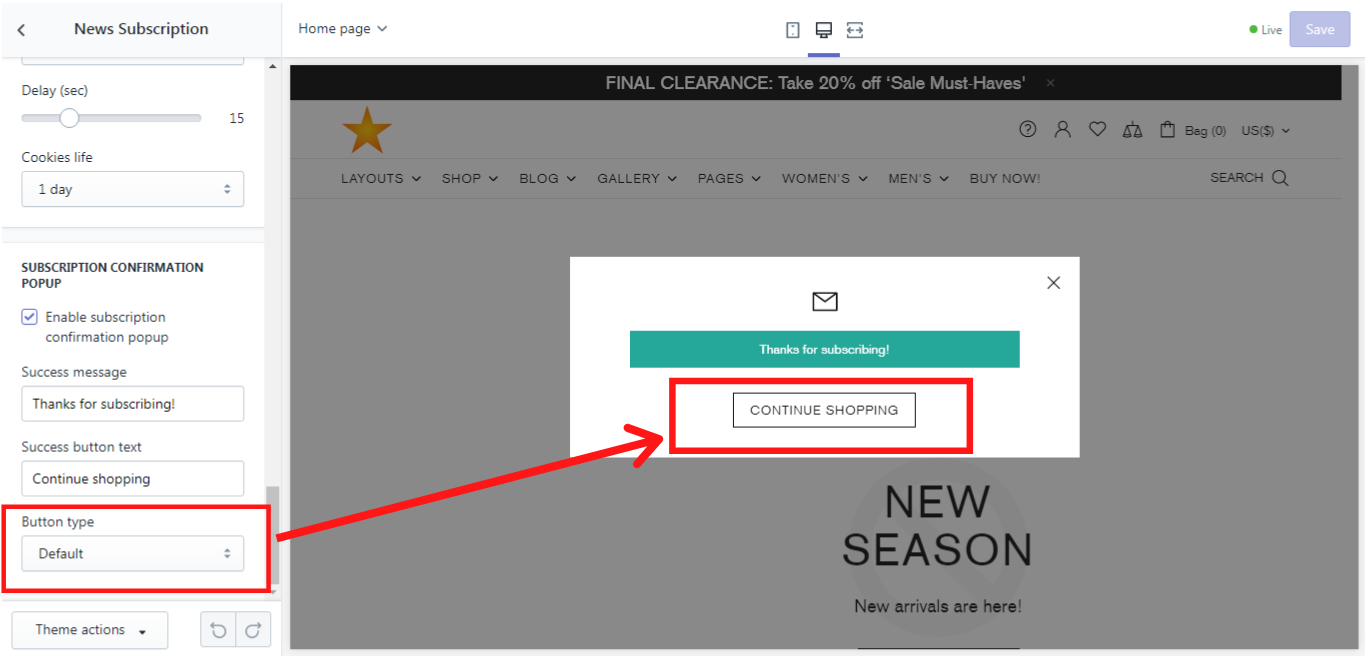
Here you can enable a subscription confirmation popup and customize it by typing your success message, e.g.: “Thank you for subscribing!” and add a success button text, e.g.: “Continue shopping”. You can also choose a button type from the default, invert, secondary and clean.
Button type
Let´s take a look at each button type.
Default:
Invert:
Secondary:
Clean: